Co se děje, když se obrázky zmenšují a zvětšují

V tomto dílu seriálu o čudlíkování si povíme o tom, jak se obrázky zvětšují a zmenšují, odkud plynou problémy, které u toho obvykle vznikají, a co se s tím dá dělat. Zabrousíme u toho trochu do matematiky a teorie signálů a seznámíme se s takovými pojmy, jako je interpolace a aliasing.

Když dojde na zvětšování a zmenšování digitálních obrázků, mnoho lidí v tom má zmatek. Příčinou je to, že dost dobře nerozlišují velikost digitálního obrázku jako takového od velikosti výstupu na monitoru nebo na papíře. Grafické editory obvykle z praktických důvodů tyhle dvě věci spolu mají propojené a pro začátečníka to může být dost matoucí. Z toho, co bylo řečeno v předchozích dílech tohoto seriálu, by ale mělo být jasné následující:

Velikost digitálního obrázku je jeho velikost v pixelech. Změnit jeho velikost znamená změnit počet pixelů. Změnu velikosti obrázku vytištěného na papíře (v centimetrech) lze ovšem provést dvěma různými způsoby. Jednak tím, že se opravdu změní rozměry digitálního obrázku a nebo tím, že se jen změní uvažované dpi pro tisk. Zatímco změna velikosti digitálního obrázku v pixelech je zásadní (a jak si ukážeme za chvíli, obecně nevratný!) zásah do digitálního obrázku, změna dpi je pouze změna kosmetická – dpi můžeme měnit libovolně, tam a zpátky, a na digitální obrázek jako takový to nebude mít vůbec žádný vliv.

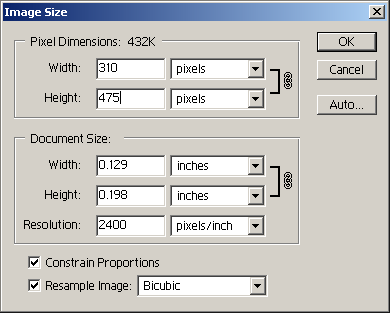
Co to znamená změnit velikost digitálního obrázku v pixelech? Představíme-li si, že je stále ještě k dispozici snímaná předloha (scéna, fotografie nebo film), pak změna počtu pixelů znamená odebrání vzorků v jiných bodech. Změně počtu pixelů se proto odborně říká převzorkování. Chceme-li proto např. ve Photoshopu změnit velikost obrázku v pixelech, musíme mít v okně, které se nám objeví poté, co zvolíme Image &gt Size (viz Obr. 1), zaškrtnunou volbu resample image (převzorkovat obraz). Velikost obrázku pak můžeme měnit přímo změnou rozměrů v pixelech nebo nepřímo, prostřednictvím změny požadovaných fyzických rozměrů dokumentu (výstupu na tiskárně). Potřebné rozměry digitálního obrázku v pixelech při daném dpi Photoshop pak sám dopočítá. Pokud tato volba zaškrtnutá není, Photoshop vlastní digitální obrázek nijak nemění, nechá vzorky tak, jak jsou. Mění se pak jen rozměry dokumentu prostřednictvím dpi, což je ale jen nezávazná, čistě formální změna – v souboru s daty se změní pouze záznam o zvoleném dpi v doprovodné hlavičce.

Obr. 1 – Okno měnění velikosti obrázku ve Photoshopu 6. Aby se velikost digitálního obrázku skutečně změnila, je potřeba mít zaškrtnutou volbu  Resample Image. Menu volby interpolace se nachází hned vedle.

Dobrá, chceme-li změnit velikost obrázku, je nutné ho převzorkovat. Jak ho ale
převzorkujeme, když snímaná předloha již není k dispozici? Hodnoty v nových bodech se odhadnou ze známých hodnot ve starých bodech. Tato klasická matematická úloha se nazývá interpolace. Smysluplná interpolace je možná za předpokladu, že se funkce, o kterou jde, nechová úplně náhodně, ale je pro ni možné vytvořit nějaký rozumný model, na jehož základě lze chybějící hodnoty odhadnout (což obrázky splňují). Nejběžněji používaným modelem jsou funkce slepené z kousků polynomů nízkého stupně. V teorii zpracování digitálních signálů zase například hraje velice důležitou roli model založený na funkcích, jejichž spektrum, získané rozkladem funkce na vlny oscilující s různou frekvencí (Fourierovou transformací), obsahuje jen jistý konečný rozsah frekvencí. A existuje spousta dalších metod interpolace založených na různých jiných modelech.

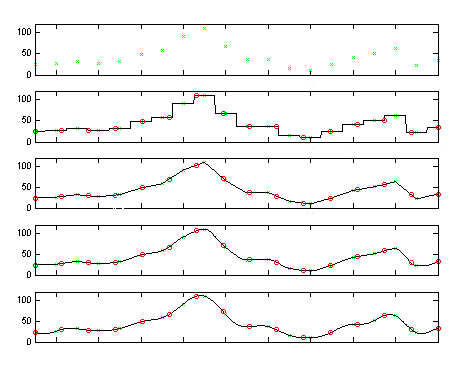
Obr. 2 – Některé základní metody interpolace funkce jedné proměnné. Příklad snížení počtu vzorků z 20 na 16. Shora dolů: 1. originální data, červený kanál náhodně zvoleného řádku obrázku (svislá osa představuje intenzitu), 2. interpolace nejbližším sousedem, 3. lineární interpolace, 4. kubická interpolace, 5. Fourierovská interpolace. Zelené křížky značí originální data, červené kroužky interpolovaná data.

Nejběžnější interpolační metody pro funkce jedné proměnné, založené na modelech zmíněných výše, jsou zachyceny na Obr. 2. U interpolace nejbližším sousedem se jako aproximace hodnoty v novém bodě vždy použije hodnota funkce v nebližším bodě, kde ji známe. Můžeme se na to dívat také tak, že se pro účely převzorkování skutečná funkce aproximuje funkcí po částech konstantní. Další možnost je použít po částech lineární aproximaci; pak se každá nová hodnota vypočte jako vážený průměr dvou známých sousedních hodnot. Nebo můžeme jít ještě dál a zvolit aproximaci kubickou, kdy se prokládá kubická křivka (polynom třetího stupně) vždy čtyřmi sousedními body. Poslední ukázka je spektrální Fourierovská interpolace, která vychází z toho, že pokud je spektrum frekvencí omezené a frekvence vzorků je alespoň dvakrát taková, jako nejvyšší frekvence zastoupená ve spektru funkce, lze tuto funkci ze vzorků zcela přesně rekonstruovat (tzv. Shannonův vzorkovací teorém, zmíněná kritická frekvence vzorkování se nazýva Nyquistova frekvence).

U převzorkovávání digitálních obrázků je princip v podstatě stejný, jen nejde o interpolaci funkce jedné, ale dvou proměnných. Interpoluje se tu současně ve dvou směrech (řádky a sloupce). Místo o interpolaci lineární, respektive kubické, pak hovoříme o interpolaci bilineární a bikubické (lineární či kubické v každém z obou směrů).
U barevných obrázků, které se skládají ze tří barevných kanálů, je navíc nutné provést interpolaci u každého z kanálů, tj. jde o interpolaci ne jen jedné, ale hned tří funkcí. Výsledná interpolovaná data se navzájem liší v závislosti na použitém modelu. Volba modelu je vždy věcí kompromisu. Pro obrázky neexistuje žádný optimální model, který by se stoprocentně shodoval s realitou. Navíc obvykle, čím lépe model vystihuje realitu, tím je komplikovanější, což znamená, že výpočty jsou náročnější a použití tohoto modelu může být z tohoto důvodu nepraktické.

Obr. 3 – Porovnání různých druhů interpolace při zvětšování obrázku. Vlevo nahoře: originální výřez, vpravo nahoře: interpolace nejbližším sousedem, vlevo uprostřed: bilineární interpolace, vpravo uprostřed: bikubická interpolace, vlevo dole: opakovaná bikubická interpolace, vpravo dole: fraktálová interpolace. Klikněte na obrázek pro nezmenšenou verzi.

Jak to vypadá v praxi? Slušné editační programy nabízejí převzorkování pomocí několika různých druhů interpolace. Například ve Photoshopu 6.0 si můžeme vybrat mezi
nejbližším sousedem, bilineární a bikubickou interpolací. Druh interpolace se nastavuje přímo v okně zvětšování/zmenšování obrázku, hned vedle volby převzorkování. Každá z těchto metod dává trochu jiné výsledky, viz Obr. 3. Nejlepší výsledky dává obvykle bikubická interpolace, a proto je též defaultní volbou. Je ale mezi třemi uvedenými početně nejnáročnější. Bilineární interpolace je úspornější a co do výsledků mezi ní a bikubickou není často zase až tak velký rozdíl. Interpolace nejbližším sousedem je sice početně velice nenáročná, ale hodí se v podstatě jen pro řídké speciální případy, kdy úmyslně chceme vytvořit obrázek sestávající se z čtverečků (např. abychom ukázali zvětšené pixely jako na ukázkách v prvním díle tohoto seriálu nebo zde na Obr. 8). Pro normální použití jsou výsledky ale obvykle příliš “zubaté”. Bilineární a hlavně bikubická interpolace více zhlazuje. To je obecně žádoucí, i když na druhou stranu zmenšený obrázek pak je o něco méně ostrý. Zmenšený obrázek je proto zpravidla dobré mírně digitálně přiostřit. Jak na to, to si povíme v jednom z dalších dílů seriálu.

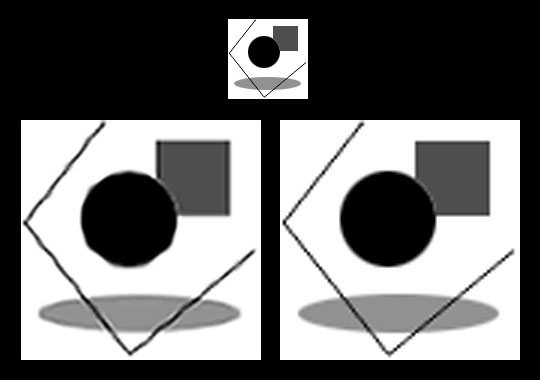
Obr. 4 – Porovnání postupného a jednorázového zvětšení obrázku. Obrázek vlevo byl zvětšován postupně, vždy o 10 pixelů. Srovnávaci obrázek vpravo byl zvětšen v jednom kroku. Bikubická interpolace.

Některé zdroje doporučují neprovádět změnu velikosti obrázku najednou, ale postupně, prostřednictvím opakovaných malých změn rozměrů (na Obr. 3 vlevo dole). Výsledkem je zvýšený kontrast podél hran (obrázek se nám pak jeví ostřejší) a menší zubatost (tou se budeme podrobněji zabývat níže). Tato metoda je ovšem velmi pracná a navíc i nespolehlivá. Efekt může být zanedbatelný nebo dokonce i negativní – v obrázku se mohou vytvořit rušivé artefakty – například se mohou vytvořit periodické textury nebo se z rovných linií může stát vlnovka,
jak je demonstrováno na Obr. 4.

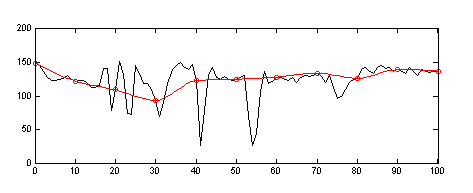
Obr. 5 – Ztráta detailů při nedostatečné hustotě vzorkování. Chybějící informaci již nelze interpolací doplnit. Originální funkce černě, interpolovaná červeně (kubická interpolace). Červené kroužky představují použité vzorky původní funkce.

Podívejme se nyní na to, jaké problémy zvětšování a zmenšování obrázků v praxi přináší. Všechny tyto problémy jsou spojené s tím, že digitální obraz je diskretizovaný, tj. zachycený pouze pomocí konečného počtu vzorků. První a nejdůležitější skutečnost, kterou je třeba si uvědomit, je, že k zachycení drobné kresby a malých detailů je zapotřebí mít dostatečný počet vzorků (toto lze přesně vyjádřit matematicky právě pomocí Nyquistovy frekvence a Shannonova vzorkovacího teorému). Musí se ale samozřejmě jednat o vzorky originální předlohy (ať už skenovaného filmu nebo papírové fotografie, či scény snímané digitální kamerou), ne o vzorky vzniklé interpolací.

Interpolace chybějící vzorky odhaduje na základě jakéhosi obecného zjednodušeného modelu a drobné individuální detaily, které původními vzorky nejsou zachycené, nemůže v žádném případě doplnit.

Toto je zachycené na Obr. 5. Zmenšení obrázku je proto obecně nevratná změna, jak už bylo zmíněno v úvodu. Tato skutečnost je názorně demonstrována na Obr. 6. Obrázek zmenšený a posléze zvětšený na původní velikost postrádá drobné detaily.

Obr. 6 – Zmenšení obrázku je zásadní a nevratná změna. Obrázek zmenšený a posléze zvětšený na původní velikost postrádá detaily. (Bikubická interpolace.)

Zvětšení je zpravidla použitelné pouze tehdy, pokud míra zvětšení je relativně malá a výsledný obraz bude např. pozorován z větší vzdálenosti, kdy absence detailů nebude tolik vadit.

Zvětšování obrázků je dobré se pokud možno vyhnout.

V současnosti pravděpodobně nejlepší technologii zvětšování obrázků nabízí rodina programů Genuine Fractals od firmy Altamira (nyní již vlastněná firmou LizardTech). Jsou to plug-iny pro Photoshop a nejsou bohužel z nejlevnějších, ale někdy bývají zdarma dodávány se skenery nebo digitálními fotoaparáty. Jedná se o fraktálovou interpolaci, respektive kombinaci fraktálů a wavelet. Možnost zvětšovat a zmenšovat obrázky je zde vedlejším produktem komprese obrazu. Fraktálová komprese byla svého času velkým hitem, ale postupem času se ukázalo, že naděje do ní vkládané jsou poněkud přehnané (proto také to spojení s waveletami v novější verzi). Nicméně princip fraktálů – podobnost funkce viděné v různých měřítcích – umožňuje obrázek zakódovaný pomocí fraktálů (ve formátu FIF nebo novějším STN) zrekonstruovat v jakémkoli zvoleném měřítku. Obrázky zvětšované pomocí programů Genuine Fractals mají ostřejší hrany a působí méně rozmazaně, než obrázky zvětšené pomocí jiných metod, jako např. bikubické interpolace (viz Obr. 3). Na druhou stranu ale zase vyrábějí ostré hrany všude, často i na místech, kde to není příliš vhodné, a také mají tendenci vytvářet nepěkné ostře ohraničené “ploché” oblasti bez textury. Ani fraktálová interpolace nedokáže zázraky. Chybějící detaily, které původní data nezachycují, dodat nedokáže.

Obr. 7 – Typické problémy při zmenšování obrázku – zubaté diagonální linie (levý horní roh) a moiré (vlevo vedle paty zadního sloupu). Zleva doprava: 1. nejbližší soused, 2. bilineární interpolace, 3. bikubická interpolace.

Problémy ale nepanují jen při zvětšování obrázků. Při zmenšování na ně narazíme také.
Jedním takovým problémem je zubatost diagonálních linií ve zmenšeném obrázku, viz Obr. 7. Zde je nutné si uvědomit, že přesné vyjádření některých geometrických tvarů na hrubé síti čtvercových pixelů je nemožné. Příkladem jsou třeba šikmé linie, viz Obr. 8. Šikmá linie bude na hrubém čtvercovém rastru vždy zubatá. Dojem zubatosti lze pouze o něco snížit pomocí použití přechodových barev (přechod ale nemůže být příliš pozvolný protože pak se jeví jako neostrost). Různé metody interpolace vytvářejí různě strmé přechody a linie ve výsledném obrázku jsou pak podle toho více či méně zubaté (a rozmazané).

Obr. 8 – Hrubý rastr čtvercových pixelů poskytuje pouze omezené možnosti pro reprezentaci geometrických útvarů. Jedním z typických prvků, který se jen obtížně reprezentuje, jsou šikmé čáry.

Další faktor, který přichází do hry, je ten, že výsledný nový vzorek se vypočítává vždy z jistého množství okolních pixelů. Pokud zmenšujeme obrázek hodně, pak se může stát, že některé pixely původního obrázku se při výpočtu nového vůbec nepoužijí – cokoli zachycovaly, se jednoduše ztratí. Pro jednoduchost uvažujme, že obrázek zmenšíme v každém směru na polovinu tak, že vypustíme každý druhý řádek a sloupec pixelů. Bude-li na obrázku tenká svislá čára tlustá přesně jeden pixel, pak můžeme dostat dva radikálně odlišné výsledky – buď je čára v lichém sloupci pixelů a pak budeme mít i ve zmenšeném obrázku čáru tlustou jeden pixel nebo je v sudém sloupci a pak po ní v novém obrázku nebude ani stopy! Pokud bude na obrázku šikmá čára, bude na zmenšeném obrázku čára přerušovaná. Dalším důsledkem jsou pak i zubaté hranice objektů. Chování různých interpolačních metod na obrázku skládajícím se z tenkých čar je zachycené na Obr. 9. Jak je demonstrováno na poslední ukázce, lze zubatost zmírnit tím, že obrázek před zmenšením mírně rozmažeme. (Pak se tenká svislá čára neztratí, ať je v obrázku kdekoli, ale místo toho dostaneme vždy méně výraznou čáru.)

Obr. 9 – Obrázek skládající se ze šikmých čar zmenšený různými technikami. Vlevo nahoře: interpolace nejbližším sousedem, vpravo nahoře: bilineární interpolace, vlevo dole: bikubická interpolace, vpravo dole: mírné rozmazání obrázku následované zmenšením pomocí bikubické interpolace.

Dalším nepříjemným efektem při zmenšování obrázků je vznik moiré v oblastech, kde je na obrázku drobná periodická textura, viz Obr. 7 a 11. K jeho vzniku dochází díky jevu nazývanému aliasing. Pokud funkci kmitající s jistou frekvencí navzorkujeme v příliš malém počtu míst, bude se nám výsledek jevit jako vzorky funkce kmitající s nižší frekvencí, viz Obr. 10. Dochází tak ke vzniku falešných frekvencí a my pak vidíme moiré, neboli různé pravidelné vzorečky, které do obrázku nepatří. Jejich vzniku lze zabránit tím, že se příliš vysoké frekvence před snížením počtu vzorků odstraní, čili obázek se před zmenšením patřičně rozmaže, stejně jako v případě zubatých linií (viz Obr. 12). Rozmazávací filtry obvykle implementované v programech pro editaci obrázků (jako např. Gaussův filtr) ovšem bohužel pro tento účel nejsou ideální.

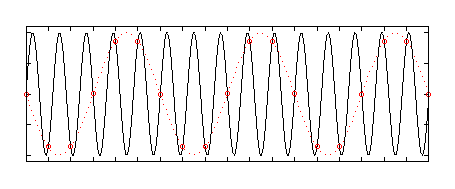
Obr. 10 – Aliasing při neodstatečně hustém vzorkování periodické funce. Původní funkce černě – červená kolečka představují zvolené vzorky. Červená tečkovaná čára je nově vzniklá falešná frekvence.

Obr. 11 – Moiré vzniklé díky aliasingu při zmenšení obrázku obsahujícího výraznou drobnou periodickou texturu. (Bikubická interpolace.)

Obr. 12 – Aliasingu je možné předejít odfiltrováním vysokých frekvencí neboli rozmazáním obrázku před zmenšením.